Homework 6: Markov Decision Processes [100 points]

Instructions

In this project, you will implement value and policy iteration. You will test your agents on Gridworld.

A skeleton file agents.py containing empty definitions for both agents is provided. You also need to download gridworld.py, which includes an MDP game Gridworld and its GUI.

You may import definitions from any standard Python library, and are encouraged to do so in case you find yourself reinventing the wheel. If you are unsure where to start, consider taking a look at the data structures and functions defined in the collections, copy, and itertools modules.

Your code will be autograded for technical correctness. Please do not change the names of any stub functions or classes within the code, or delete any functions we asked you to implement. You can add helper functions if needed.

Once you have completed the assignment, you should submit your file on Gradescope. You may submit as many times as you would like before the deadline, but only the last submission will be saved.

0. Gridworld

Your agents will be given an MDP game, Gridworld.

In a Gridworld, each state is a tuple of integers \((x, y)\), corresponding to the coordinates on the grid. And for each non-terminal state, there are exactly four actions, going UP, DOWN, LEFT, or RIGHT. Gridworld also has two parameters, noise and living_reward.

noise defines the probability of the robot not doing exactly what you tell it to do. For example, if you tell the robot to go UP, the probability of it actually going up is $1-\text{noise}$; the probability of the agent going the perpendicular direction LEFT or RIGHT are both \(\frac{\text{noise}}{2}\). Furthermore, if the robot is hitting a wall, then the outcome state will still be the same state, because the robot didn’t move at all. By default, noise is \(0.2\).

living_reward defines the reward given to the robot for each action that leads to a non-terminal state. By default it’s \(0\), so no reward given to the agent before reaching the terminal states.

However, your agents should be as generic as possible, and should not assume anything related to Gridworld in your agents. In fact, you should not import gridworld.py into your agents.py. Instead, you agents shall take in a generic game object at initialization, with game implementing the following interface:

class MDPGame:
    states: Set[State]
    get_actions(state: State) -> Set[Action]
    get_transitions(current_state: State, action: Action) -> Dict[State, float]
    get_reward(current_state: State, action: Action, next_state: State) -> float

• game.states is a set of non-terminal States in the game. A State is guaranteed hashable.
• game.get_actions(state) takes in a State, and returns a set of all possible Actions the agent can do in that state. If the state is a terminal state, then an empty set will be returned.
• game.get_transitions(current_state, action) takes in the current State and the Action the agent wants to execute. It then returns a mapping of the outcome states to the probability of arriving at that state. Note: you can use .items() on a dictionary to get a list of (k, v) pairs.
• game.get_reward(current_state, action, next_state) takes in the current State, the Action, and the outcome State, and returns the reward as a real number.

1. Value Iteration [45 Points]

Write a value iteration agent in class ValueIterationAgent, which has been partially specified for you in agents.py.

ValueIterationAgent takes in an MDP game and the discount factor \(\gamma\) on construction. It then should initialize all the state values to $0$ (i.e. \(V_0(s) =0\)). You need to implement the following methods for ValueIterationAgent using current estimated values \(V^*\), which is \(V_0\) at the beginning.

• agent.get_value(state) returns the value of the state, \(V^*(s)\).
• agent.get_q_value(state, action) returns the q-state value of the (state, action) pair, \(Q^*(s, a)\).
• agent.get_best_policy(state) returns the best policy of the state, \(\pi^*(s)\).

Then, once you implemented these, you can implement agent.iterate(), which it to iterate only once using Bellman equations, and store the new $V_{k+1}$ in place of $V^*$.

Important: Use the “batch” version of value iteration where each vector \(V_{k+1}\) is computed from a fixed previous state \(V^*\) (like in lecture), not the “online” version where one single weight vector is updated in place. The difference is discussed in Sutton & Barto in the 6th paragraph of chapter 4.4.

For more instructions, refer to the lecture slides and comments in the skeleton file.

The following command loads your ValueIterationAgent:

python3 gridworld.py

In the GUI, you will see the current agent type displayed on the top. You should also see the current number of iteration on the top, the game board in the middle, and a selection of the current view mode on the bottom.

The terminal states are displayed with a color (either green or red) and the rewards are displayed in a bold font. The block in yellow is the starting state, and the blocks in completely black are non-existing states (walls) in the game. Other blocks are non-terminal states.

By changing the number of iterations on the top, you can view the state values, q-state values and policies your agent returns after running the $i$th iteration. You should expect to see all state values \(V^*(s)\) being $0$ at the $0$th iteration.

Hint: On the default BookGrid, running value iteration for 5 iterations should give you the output below.

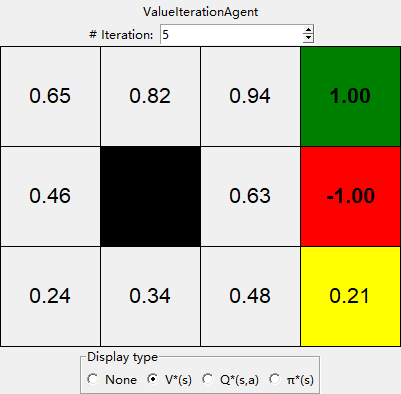
Your value iteration agent will be graded on a new grid. We will check your values, q-state values, and policies after fixed numbers of iterations and at convergence (e.g. after 100 iterations).

2. Policy Iteration [25 Points]

To implement PolicyIterationAgent, you need to fix the policy \(\pi^*\) at the beginning of policy iteration, and then keep iterating \(V^{\pi^*}(s)\) until it converges (the biggest difference between the current iteration \(V^{\pi^*}_{k}(s)\) and the last iteration \(V^{\pi^*}_{k-1}(s)\) is less than \(\epsilon = 10^{-6}\)). You then can then update \(V^*(s)\) to the converged \(V^{\pi^*}(s)\) and claim the end of one policy iteration.

All other values (Q-state values, policies) should be calculated the same way as ValueIterationAgent, and the only difference is at the iterate() method. However, if you need to implement helper functions or override ValueIterationAgent’s methods, you can add them as well.

The following command loads your PolicyIterationAgent:

python3 gridworld.py -a policy

Hint: You should see the same value for ValueIterationAgent and PolicyIterationAgent after they converge, and PolicyIterationAgent should converge much faster than the ValueIterationAgent.

Your policy iteration agent will be checked the same way as your value iteration agent.

3. Bridge Crossing Analysis [10 Points]

BridgeGrid is a grid world map with a low-reward terminal state and a high-reward terminal state separated by a narrow “bridge,” on either side of which is a chasm of high negative reward. The agent starts near the low-reward state (the yellow block). With the default discount of \(0.9\) and the default noise of \(0.2\), the optimal policy does not cross the bridge. Change only ONE of the discount or the noise parameters so that the optimal policy causes the agent to attempt to cross the bridge. Put your answer in bridge_crossing() of agents.py.

To change the discount or noise in Gridworld GUI, use --discount or --noise. To use the bridge grid, add bridge to the end of the command line. The default parameter corresponds to:

python3 gridworld.py --discount 0.9 --noise 0.2 bridge

4. Policies [15 Points]

Consider the DiscountGrid layout, shown below. This grid has two terminal states with positive payoffs (in the middle row), a close exit with payoff +1 and a distant exit with payoff +10. The bottom row of the grid consists of terminal states with negative payoffs (shown in red); each state in this “cliff” region has payoff -10. The starting state is the yellow square. We distinguish between two types of paths:

1. paths that “risk the cliff” and travel near the bottom row of the grid; these paths are shorter but risk earning a large negative payoff, and are represented by the red arrow in the figure below.
2. paths that “avoid the cliff” and travel along the top edge of the grid. These paths are longer but are less likely to incur huge negative payoffs. These paths are represented by the green arrow in the figure below.

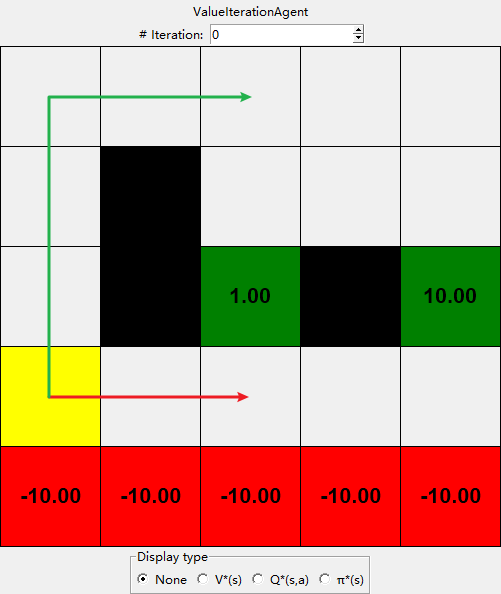
In this question, you will choose settings of the discount, noise, and living reward parameters for this MDP to produce optimal policies of several different types. Your setting of the parameter values for each part should have the property that, if your agent followed its optimal policy without being subject to any noise, it would exhibit the given behavior. If a particular behavior is not achieved for any setting of the parameters, assert that the policy is impossible by returning the string ‘NOT POSSIBLE’. The default corresponds to:

python gridworld.py --discount 0.9 --noise 0.2 --living-reward 0.0 discount

Here are the optimal policy types you should attempt to produce:

1. Prefer the closer exit (+1), risking the cliff (-10)
2. Prefer the closer exit (+1), but avoiding the cliff (-10)
3. Prefer the distant exit (+10), risking the cliff (-10)
4. Prefer the distant exit (+10), avoiding the cliff (-10)
5. Avoid both exits and the cliff (so an episode should never terminate)

Questions 4a through question 4e should each return a 3-item tuple of (discount, noise, living reward) in analysis.py, or string ‘NOT POSSIBLE’ if it’s impossible to achieve.

Note: You can check your policies in the GUI. For example, using a correct answer to 4a, the policy in the starting state should point to the right, the policy to its right should also point to the right, and the policy below terminal state \(1.00\) should point up.

To quickly get to the converged policy, you can use --iteration option. For example

python gridworld.py --iteration 100 discount

Will begin the GUI on the 100th iteration.

5. Feedback [5 points]

1. [1 point] Approximately how many hours did you spend on this assignment?

2. [2 point] Which aspects of this assignment did you find most challenging? Were there any significant stumbling blocks?

3. [2 point] Which aspects of this assignment did you like? Is there anything you would have changed?